PROBLEM SOLVING AND PYTHON PROGRAMMING

PROBLEM SOLVING AND PYTHON PROGRAMMING

---

UNIT I – ALGORITHMIC PROBLEM SOLVING

Introduction to problem solving

          A computer is an electronic device capable of executing programs. A program is an organized set of instructions. Each program performs a specific task when executed by the computer. A program is usually written in a programming language like C, C++, Java, Python etc.

The primary aim of a computer program is to solve a given problem. Any problem, irrespective of the programming language in which it is written, has three aspects

1.    Output – What is the desired outcome of the program?

2.    Input – What is the available data / information?

3.    Process – How the input information can be processed / manipulated to produce the desired output?

Figure 1.1: Execution of a Program.

Algorithm

An algorithm is a step-by-step procedure to solve a given problem. It is a well-defined computational procedure that takes some values as input, manipulates them using a set of instructions and produces some values as output and terminates in a finite amount of time. An algorithm, when formally written in a programming language is called a program, or code.

Derivation of an algorithm that solves the problem and conversion of the algorithm into code, together, is known as Algorithmic Problem Solving.

Characteristics of an Algorithm

1.  Well defined – the steps are in a clear order

2.  Unambiguous and exact – the operations in the algorithm must be precisely described such that they are understood by a computing agent without  further simplification and there remains no uncertainty

3.  Effectively computable – the computing agent can actually carry out the operation and provide the correct answer to the problem

4.  Terminate – The purpose of an algorithm is to solve a problem. If the program does not stop when executed, we will not be able to get any result from it. Therefore, an algorithm must contain a finite number of steps in its execution.

5.  General – An algorithm must solve every instance of the problem. For example, a program that computes the area of a rectangle should work on all possible dimensions of the rectangle, within the limits of the programming language and the machine.

Method for Developing an Algorithm

1.  Define the problem: State the problem you are trying to solve in clear and concise terms.

2.  List the  Inputs (information needed to solve the problem) and the outputs (what the algorithm will produce as a result)

3.  Describe the steps needed to convert or manipulate the inputs to produce the outputs. Start at a high level first, and keep refining the steps until they are effectively computable operations.

4.  Test the algorithm: choose data sets and verify that your algorithm works

Building blocks of algorithms

Any algorithm can be constructed from just three basic building blocks. These three building blocks are Sequence, Selection (Branching), and Repetition (Looping / Iteration) and are collectively called as Control Structures. Control structures control the direction of flow of the program. It determines how a computer will respond when given certain conditions and parameters.

Decision steps

Selection and repetition statements typically involve decision steps based on an expression evaluation. Expression may involve numeric value, arithmetic, logical and relational operators. Decision steps are commonly called as test conditions.

In case of arithmetic operators, expression that evaluates to a value can be interpreted as a true / false condition. The rule is: If an expression evaluates to 0, its truth value is false and if an expression evaluates to non-zero value, its truth value is true. Example if a = 7, and b = 5,

Expression	Value
a	True
a – b	True
a – 7	False

Relational operators evaluate to a Boolean value. Example if a = 5, and    b = 3, then (a > b) will evaluate to true.  Similarly (a < b) will evaluate to false. Logical operators are generally used to combine multiple conditions in the same expression. It may involve any types of operators. Example a = 5, b = 7 & c = 3

Expression	Value
(a > b) AND (a > c)	True
(a + b) OR (a – c)	True

Sequence Structure:

The sequence structure is the default structure. It contains a sequence of statements placed one after the other and is executed in the same order.

Selection Structure:

Selection structure is used for choosing between two or more alternative blocks of code. It is a binary decision based on whether an expression (also called as test condition) evaluates to TRUE or FALSE. Given two alternative blocks, if the test condition evaluates to true, one of the two branches is explored; if the condition is false, the other alternative is taken. The commonly used selection structures in any programming language are ‘IF’, ‘IF – ELSE’ and ‘SWITCH’

IF structure: if the condition evaluates to true, the statements in the block will be executed. Else it will be skipped and the program continues its execution from the statement after the end if statement.

Syntax:

if condition then

   (statements)

end if

IF – ELSE Structure: Binary condition where only one block of statements will be executed. If the condition evaluates to true, the statements in the if-block will be executed. If the condition evaluates to false, the statements in the else block will be executed.

Syntax:

if condition then

   (statements)

else

    (other statements)

end if

IF – ELSE – IF Structure: By using if-elseif-else, it is possible to combine several conditions. Only the statements following the first condition that is found to be true will be executed. All other statements will be skipped.

Syntax:

if condition then

   (statements)

elseif condition then

    (more statements)

elseif condition then

    (more statements)

...

else

    (other statements)

end if

Switch Structure: This is a multi-way branching statement, where, based on a condition, the control is transferred to one of the many possible points. Keywords used in programming languages to implement switch statement include switch, case, select or inspect. This is implemented as:

switch (value) then

case value-1: // Statement block

case value-2: // Statement block

case value-3: // Statement block

…

default: // statement block

end switch

Repetition Structure:

Repetition structure is used for looping, i.e. repeating a block of code multiple times in a row. It is a construct where statements can be executed repeatedly until a condition evaluates to TRUE or FALSE. It is represented by the ‘while’, ‘do-while’ and ‘for’ constructs in most programming languages.

WHILE Structure: The while construct consists of a block of code and a test condition. The test condition is evaluated, and if it evaluates to true, the code within the block is executed. This repeats until the test condition becomes false. Because the while loop checks the test condition before the block is executed, the while control structure is often also known as an entry-controlled loop. If the test condition evaluates to false the first time, the statement block may never be executed.

Syntax:               while (test-condition) then

// Statement block

end while

DO – WHILE Structure: The do while construct consists of a statement block and a test condition. First, the code within the block is executed, and then the condition is evaluated. If the condition is true the code within the block is executed again. This repeats until the condition becomes false. Because do while loops check the condition after the block is executed, the control structure is often also known as an exit-controlled loop. In contrast to while loop even if the test condition evaluates to false the first time itself, the statement block is executed at-least once.

Syntax:                  do

// Statement block

while (test-condition)

FOR Structure: While and do-while loop are used in situations where the number of times the loop is to be executed is unknown. For structure in contrast is used in situation where number of times the loop is to executed is deterministic. The general syntax of the For structure contains an initialization value, a test condition and an increment value.

Syntax:                  for (initialization; Test condition; increment)

                                      // statement block

                             End for;

Iteration and Recursion:

One complete execution of a loop is called iteration. Unbounded loops (while and do-while) refer to those whose number of iterations depends on the eventuality that the termination condition is satisfied. If the condition for the termination of the loop is not satisfied after some finite number of iterations it ends up as an infinite loop. Bounded loops (for) refer to those whose number of iterations is known before-hand.

A recursive algorithm is an algorithm which calls itself with smaller input values, and which obtains the result for the current input by applying simple operations to the returned value for the smaller input. More generally if a problem can be solved utilizing solutions to smaller versions of the same problem, and the smaller versions reduce to easily solvable cases, then one can use a recursive algorithm to solve that problem.

Nested Structures:

Combining the use of these control structures, for example, a loop within a loop (nested loops), a branch within another branch (nested if), a branch within a loop, a loop within a branch, and so forth, is not uncommon. Complex algorithms may have more complicated logic structure and deep level of nesting.

Example 1: Algorithm to find minimum, maximum & average of list of numbers

1.  First, initialize sum to zero, min to a very big number, and max to a very small number.

2.  Then, enter the numbers, one by one.

3.  For each number that you have entered, assign it to num and add it to the sum.

4.  At the same time, compare num with min, if num is smaller than min, let min be num instead.

5.  Similarly, compare num with max, if num is larger than max, let max be num instead.

6.  After all the numbers have been entered, divide sum by the numbers of items entered, and let avg be this result.

7.  End of algorithm.

Example 2: The modern Euclidean algorithm to compute the GCD (Greatest Common Divisor) of two integers:

1.    Let A and B be integers with A > B ≥ 0.

2.    If B = 0, then the gcd is A and the algorithm ends.

3.    Otherwise, find q and r such that

A = qB + r where 0 ≤ r < B

Note that we have 0 ≤ r < B < A and gcd(A,B) = gcd(B,r).

Replace A by B, and B by r. Go to step 2.

PSEUDOCODE

Pseudocode or Program Design Language

The word "pseudo" means "false," so "pseudocode" means "false code." Pseudocode is one of the initial processes in the program development. It is the outline of a program written in natural language that precisely describes the steps to be taken to complete a program. It is an informal way of describing the key principles of a program making it easier to understand the underlying logic and flow of the program.

Pseudocode provides an efficiently detailed yet readable description of what a computer program is expected to do. It avoids language-specific elements and is written such that the desired programming code can be generated almost automatically from each statement. In computer program development, pseudocode is extensively used for sketching out the structure of the program before the actual coding takes place. Since the logic and flow of the program and data are already defined, the programmer can focus on the coding, resulting in faster code development.

Basic Guidelines to create pseudocode:

1.  Do not use language-specific commands. Pseudocode should be universal and written such that it can be translated into any language.

2.  Write only one task or statement per line. Including too much information on one line can be confusing and increases the possibility of errors.

3.  Capitalize keywords. Example - 'Read,' 'Write,' or 'Display'. This helps to identify key commands when coding in a specific language.

4.  Use proper indents in control structures to make it easier to read the program and identify the flow of the program.

Advantages of pseudocode

1. Easy to write: Pseudocode is language independent. It does not use any programming language syntax. It uses natural language and is hence can be written easily and quickly in any word processor.

2. Easy to: Programming languages are difficult to read for most people, but pseudocode allows nonprogrammers, such as business analysts, to review the steps and confirm that the proposed code matches the client requirements.  

3. Easy to read, understand check for errors: Pseudocode is both detailed and readable. It can be checked by designers and programmers to study the program / data flow and ensure that it matches the design specifications.

4. Error Check: Pseudocode provides an additional level at which inspection can be performed. It helps to check for conceptual errors and trap defects before they become code. This also increases the product reliability.

5. Easy to convert to program: Pseudocode is an outline of the program. The format of pseudocode is similar to that of the programs. Both pseudocode and program consists a set of sequential statements and use defined set of keywords. Therefore, pseudocode can be converted to a full-fledged program using the syntax any programming language.

6. Impose increased discipline on the process of documenting the design.

7.  Helps in faster code development, since the logic and program / data flow are already defined.

8.   Comparison with flow chart:

a.  Flowchart may run for multiple pages. Pseudocodes are more compact.

b.  Not easy to modify a flowchart. Can easily make changes in pseudocode.

Limitations of Pseudocode

1. There is no defined standard for writing pseudocode. Hence pseudocode is by nature unstructured and programmers may use their own styles.

2. While pseudocode is easy to read, it is not visual. It does not provide as good a map for the programmer as a flowchart does.

3.  For a beginner, it is easier to follow complex logic when drawn as a flowchart, rather than when written in pseudocode.

4.  Since pseudocode focus on detailed description, a lot of practice and concentration is required to write pseudocode as compared to flowchart

5.  Creates an additional level of documentation to maintain.

Guidelines for writing pseudocode:

1.   State the name of programmer

2.   State the date

3.   State the name of the subroutine.

4.   Give a brief description of the function of the subroutine/program.

5.   Input: State the names of the input variables, their types, and give a brief description for each.

6.  Output: State the names of the input variables, their types, and give a brief description for each

7.   Algorithm: Generally pseudocode is written between begin and end statements. A comment entry is used to provide information about the steps used in the pseudocode. Commonly used keywords in pseudocode to denote various programming process are

§  Comment               :    //

§  Input                     :    READ, GET, OBTAIN, PROMPT, ACCEPT

§  Output                  :    PRINT, DISPLAY, SHOW

§  Initialize                :    SET, INITIALIZE

§  Compute                :    COMPUTE, CALCULATE

§  Add one                :    INCREMENT

§  Function call          :    CALL <Subroutine_name>

Common Operator Symbols in Pseudocode

The following table shows some of the common operators used in writing pseudocode.

Type of operation	Symbol	Example
Arithmetic	+, −, ×, /, mod	Area ← length x breadth
Relational or Comparison	=, ≠, <, >, ≤, ≥	a ≤ b
Logical	and, or	a > b and a > c
Assignment	← or :=	c ← 2πr, c := 2πr
Floor/ceiling	⌊, ⌋, ⌈, ⌉	a ← ⌊b⌋,  a ← ⌈b⌉
Sums, products	∑ ∏	h ←

Table 1.1: Operators in pseudocode

Pseudocode Language Constructs

1.    Input / Output

a.    Input: Get var1, var2, ...

b.    Output: Display var1, var2, ...

c.    Initialize:  c := 5, pi ← 3.142

2.    Computation / Assignment

a.    Compute var1 as the sum of x and y

b.    Assign expression to var2

c.    Increment counter1

3.    Selection

a.    Single-Selection IF

                                         i.    IF condition THEN (IF condition is true, then do subordinate statement 1, etc. If condition is false, then skip statements)

1.    statement 1

2.    etc.

b.   Double-Selection IF – ELSE

                                         i.    IF condition THEN (IF condition is true, then do subordinate statement 1, etc. If condition is false, then skip statements and execute statements under ELSE)

1.    statement 1

2.    etc.

                                       ii.    ELSE (else if condition is not true, then do subordinate statement 2, etc.)

1.    statement 2

2.    etc

c.    SWITCH expression TO

                                         i.    case 1: action1

                                       ii.    case 2: action2

                                      iii.    etc.

                                      iv.    default: action

4.    Repetition

a.    FOR structure (a specialized version of WHILE for repeating execution of statements a specific number of times)

                                         i.    FOR bounds on repetition

1.    statement 1

2.    etc.

b.    WHILE condition (while condition is true, then do subordinate statements)

                                         i.    statement 1

                                       ii.    etc.

c.    DO – WHILE structure (like WHILE, but tests condition at the end of the loop. Thus, statements in the structure will always be executed at least once.)

                                         i.    DO

1.    statement 1

2.    etc.

                                       ii.    WHILE condition

Example: Pseudocode to find the minimum, maximum, and average of a list of numbers

Programmer:  IT_Dept

Date:  01.07.2017

Name: Number_manipulation

Function: Find minimum, maximum and average in a list of numbers.

Input: List of numbers

Output: minimum, maximum, and average of the given list of numbers.

FLOWCHARTS

Flow charts

Flowchart is a graphical tool that diagrammatically depicts the steps and structure of an algorithm or program. A flowchart consists of a collection of symbols. Some of the frequently used symbols are explained below.

§  Terminal symbols and Predefined process symbols

o   All flow charts start with a Terminal or Predefined Process symbol.

o   Only one flow line is used with these symbols.

o   Terminal symbols indicate the start or end of a program.

Figure 1.2: Terminal symbol

o   Predefined process symbols are used to invoke a subroutine or an interrupt program.

Figure 1.3: Predefined process symbol

§  Flow lines

o   Collection of arrows that indicate the direction of the progression of the program. Intersection of flow lines should be avoided to make the flow chart more effective

Figure 1.4: Flow lines

§  Input / Output Symbols

o   Represents input and output of data

Figure 1.5: Input / Output symbol

Figure 1.6: Manual Input Symbol

§  Process symbols

o   Represents any type of internal operation, including data transformation, data movement, logic operation, etc.

o   Only one flow line should exit a process symbol.

Figure 1.7: Process symbol

§  Documents

o   Indicates data that can be read by people, such as printed output.

Figure 1.8: Single Document symbol

Figure 1.9: Multiple Document symbol

§  Decision symbols

o   Usually, evaluates a condition or statement and branches depending on whether the evaluation is true or false

o   Only one flow line should enter a decision symbol. But two or three flow lines may leave the decision symbol.

Figure 1.10: Decision symbol

§  Manual loop:

o   Indicates a sequence of commands that will continue to repeat until stopped manually

Figure 1.11: Manual loop Symbol

§  Delay

o   Indicates a delay in the process

Figure 1.12: Delay Symbol

§  Connector symbols

o   Connects sections of the flowchart, so that the diagram can maintain a smooth, linear flow.

o   Connectors are commonly used to connect breaks in the flowchart. Examples include:

§  From one page to another page.

§  From the bottom of the page to the top of the same page.

o   In case of complex flow charts, connectors are used to reduce the number of flow lines.

§  Example – An upward flow of more than 3 symbols

Figure 1.13: Connector symbol

§  Off Page Connector

o   Creates a cross reference and hyperlink from a process on one page to a process on another

Figure 1.14: Off Page Connector

§  Annotation

o   Provides additional information about a flow chart symbol. Generally used to describe the data or process more clearly

Figure 1.15: Annotation symbol

§  Magnetic disk

o   Indicates a list of information with a standard structure that allows for searching and sorting

Figure 1.16: Magnetic disk symbol

§  Stored data

o   Indicates any type of stored data

Figure 1.17: Stored Data Symbol

§  Internal storage

o   Indicates an internal storage device

Figure 1.18: Internal Storage Symbol

§  Collate

o   Indicates an step that organizes data into a standard format

Figure 1.19: Collate Symbol

§  Merge

o   Indicates a step that merges multiple sets into one

Figure 1.20: Merge Symbol

§  Sort

o   Indicates a step that organizes items list sequentially

Figure 1.21: Sort Symbol

Flowchart for control structures

Sequence Structure:

Figure 1.22: Flowchart for Sequence structures

Selection structures:

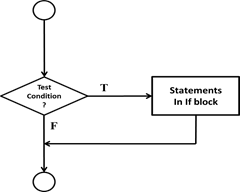
Figure 1.23: Flowchart – If structure

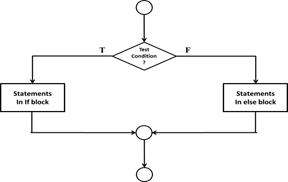
Figure 1.24: Flowchart – If – else Structure

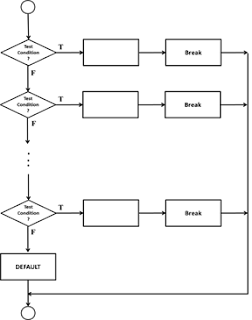
Figure 1.25: Flowchart – Switch Structure

Repetition Structures:

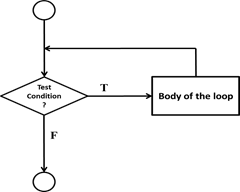
Figure 1.26: Flowchart – While Loop

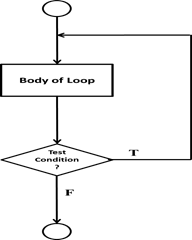
Figure 1.27: Flowchart – DO – While Loop

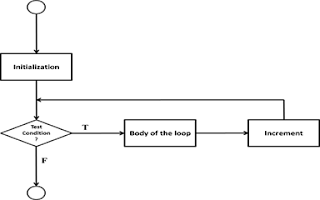
Figure 1.28: Flowchart – For Loop

General rules for drawing flowcharts

1. Flowcharts should be clear, neat and easy to follow.

2. Flowcharts are drawn such that flow generally goes from top to bottom.

3. All flow charts start with a Terminal or Predefined Process (for interrupt programs or subroutines) symbol.

4. All flowcharts end with a terminal or a contentious loop.

5. All symbols of the flowchart are connected by flow lines

6. Flow lines enter the top of the symbol and exit out the bottom, except for the Decision symbol, which can have flow lines exiting from the bottom or the sides

7. Subroutines and Interrupt programs have their own and independent flowcharts.

Benefits of flow charts:

1. Makes logic clear – provides a pictorial representation of the task. Makes the logic easier to follow

2. Communication – being a graphical representation of a problem solving logic, flow charts are a better way of communicating the logic of a system.

3. Effective analysis: the problem can be analyzed in an effective way with the help of a flow chart.

4. Useful in coding: flow charts act as a guide or blue print during the analysis and program development phase

5. Proper testing and debugging – helps in detecting the errors in a program

6. Appropriate documentation – flow charts serve as a good program documentation tool

Limitations of flow charts:

1. Complex – when a program is very large the flowchart may continue for many pages, making them hard to follow

2. Costly – drawing flow charts are viable only if the problem solving logic is straight forward. And not very lengthy

3. Difficult to modify – due to its symbolic nature, any change or modification to a flow chart usually requires redrawing the entire logic again and redrawing a complex flow chart is not a simple task.

4. No update – usually programs are updated regularly. However the the corresponding update of flow chart may not take place especially in case of large programs

Flowchart of a program to find the minimum, maximum, and average of a list of numbers

 

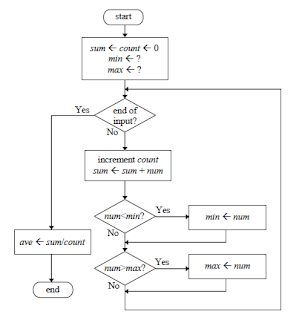
Figure 1.29: Flowchart for program to find the minimum, maximum, and average of a list of numbers Loop